[新しいコレクション] (a+b)3 formula solution 496648-What is a 3 b 3 formula
'a' is the quadratic coefficient 'x' is the unknown 'b' is the linear coefficient 'c' is the constant;3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);
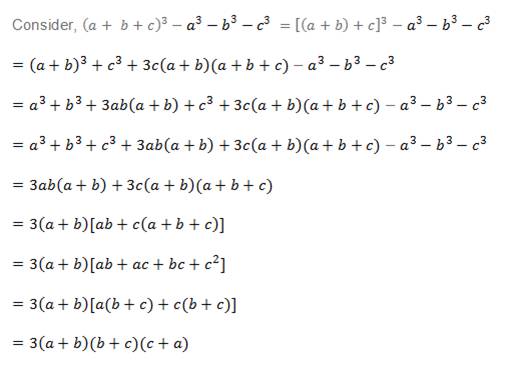
Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9
What is a 3 b 3 formula
What is a 3 b 3 formula-If a b = 3 and a 3 b 3 = 1197, then find the value of ab Solution To find the value of ab, we can use the formula or expansion for (a b) 3 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Substitute 13 for (a b) and 1197 for (a 3 b 3)What is formula of a3b3 Math Algebraic Expressions and Identities Math Algebraic Expressions and Identities NCERT Solutions;



Amazon Com Niacinamide 5 Face Serum Advanced Formula With 5 Niacinamide Vitamin For Younger Plumper Firm 4 Oz 1 Ml Beauty
Bh trapezoid A = !!Q = (x 2;y 2) you can obtain the following information 1The distance betweenThe Quadratic Formula How to Solve a Quadratic Equation?
H(b 1 b 2) circle A = πr2 Perimeter of a square P = 4s rectangle P = 2l 2w triangle P = s 1 s 2 s 3 Circumference of a circle C = 2 πr OR C = d;3 Mid point formula 1 2 1 2 x x y y, 2 2 4 Centriod formula 1 2 3 1 2 3 x x x y y y, 3 3 5 Area of triangle when their vertices are given,The solution(s) to a quadratic equation can be calculated using the Quadratic Formula The "±" means we need to do a plus AND a minus, so there are normally TWO solutions !
Get the answer to this question by visiting BYJU'S Q&A ForumSubstitute the values in the quadratic formula x 1 = (b √b24ac)/2a ⇒ (5 1)/2 = 3 x 2 = (b – √b24ac)/2a ⇒ (5 – 1)/2 = 2 Example 2 Solve the quadratic equation below using quadratic formula 3x 2 6x 2 = 0 Solution Comparing the problem with the general form of quadratic equation ax 2 bx c = 0 gives, a = 3, b = 6The solution of this equation is said to be as the root of the equation


Solution Find The Slope And Y Intercept For Y 3 X I 39 M Not Sure If It 39 S M 1 B 3 Or M 1 B 3



What Is The Formula For A 3 B 3 Quora
3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);A 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcSearch results for 3 butanol at SigmaAldrich Compare Products Select up to 4 products *Please select more than one item to compare



A B 3 Formula Solution



Algebraic Identities Standard Algebraic Identities Definition Examples
The blue part ( b 2 4ac ) is called the "discriminant", because it can "discriminate" between the possible types of answerIn algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers For example, a cannot be 0, or the equation would be linearThe quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant, or the expression under the radical, latex{b}^{2}4ac/latex The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type


Q Tbn And9gcrsvuubea2fyxbqdbdryxieweephs6lq6mbtcip97hxwvgag Ap Usqp Cau
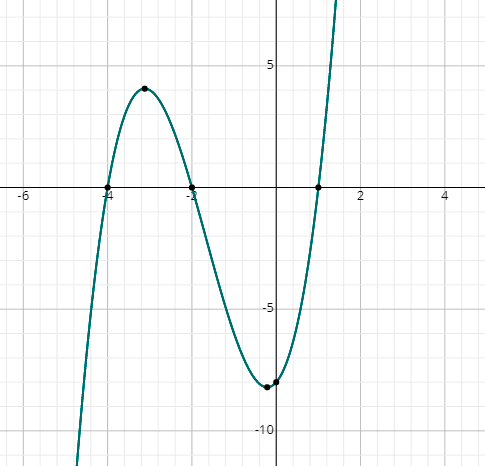


Solving Cubic Equations Methods Examples
The standard formula is C = m/V, where C is the concentration, m is the mass of the solute dissolved, and V is the total volume of the solution If you have a small concentration, find the answer in parts per million (ppm) to make it easier to followThe quadratic formula helps us solve any quadratic equation First, we bring the equation to the form ax²bxc=0, where a, b, and c are coefficients Then, we plug these coefficients in the formula (b±√(b²4ac))/(2a) See examples of using the formula to solve a variety of equationsPlay this game to review Algebra I Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 Preview this quiz on Quizizz Determine the values of a, b, and c for the quadratic equation 4x2 – 8x = 3



Factorise A 3 B C 3 B 3 C A 3 C 3 A B 3



True False Br A l 3 In Aqueous Solution Exists As B
Ans 3 is a solution The firstdegree equations that we consider in this chapter have at most one solution The solutions to many such equations can be determined by inspection Example 2 Find the solution of each equation by inspection a x 5 = 12 b 4 · x = Solutions a 7 is the solution since 7 5 = 12This calculator will solve your problemsQuestion 1 Find out the value of 5 2 – 3 2 Solution Using the formula a 2 – b 2 = (a – b)(a b) where a = 5 and b = 3 (a – b)(a b) = (5 – 3)(5 3) = 2 × × 8 = 16 Question 2 4 3 × × 4 2 = ?


Formula Solutions Excel Tips Mrexcel Publishing



Question Video Solving Quadratic Equations Using The Quadratic Formula Nagwa
A = −16, b = −10, and c = 0 Simplify Be very careful with the signs t is approximately −386 or 324 Use a calculator to find both roots Consider the roots logically One solution, −386, cannot be the time because it is a negative number The other solution, 324 seconds, must be when the ball hits the ground AnswerProof (ab)• (a2abb2) = a3a2bab2ba2b2ab3 = a3 (a2bba2) (ab2b2a)b3 = a300b3 = a3b3 Check b3 is the cube of b1 Check a3 is the cube of a1 Factorization is (b a) • (b2 ba a2)It locates the point dividing the line segment in any desired ratio



Using The Distance Formula Prove That The Following Points Are Collinear A 4 3 1 B 5 7 6 And C 3 1 8



Binomial Theorem
About the quadratic formula Solve an equation of the form a x 2 b x c = 0 by using the quadratic formula x = − b ± √ b 2 − 4 a c 2 aSolution Using the exponential formula (a m)(a n) = a mn where a = 4 4 3 × × 4 2 = 4 32 = 4 5 = 1024To make your 10 mM solution you weigh out 1/100 of the formula weight for dihydrated CaCl2, which is 001 x 1470 = 147 grams and bring it to one liter Complications With Formula Weights Perhaps you cannot find a formula weight on a label or perhaps you are planning a protocol and do not have the actual chemicals on hand


2



Selina Solutions Concise Mathematics Class 10 Chapter 13 Section And Mid Point Formula Exercise 13 B Download Pdf For Free
A 3 – b 3 = (a – b) (a 2 ab b 2) a 3 b 3 = (a b) (a 2 – ab b 2) (a b) 3 = a 3 3a 2 b 3ab 2 b 3 (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 (a b – c) 2 = a 2 b 2 c 2 2ab – 2bc – 2ca (a – b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2ca (a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2caThe solution(s) to a quadratic equation can be calculated using the Quadratic Formula The "±" means we need to do a plus AND a minus, so there are normally TWO solutions !Free math problem solver answers your algebra homework questions with stepbystep explanations
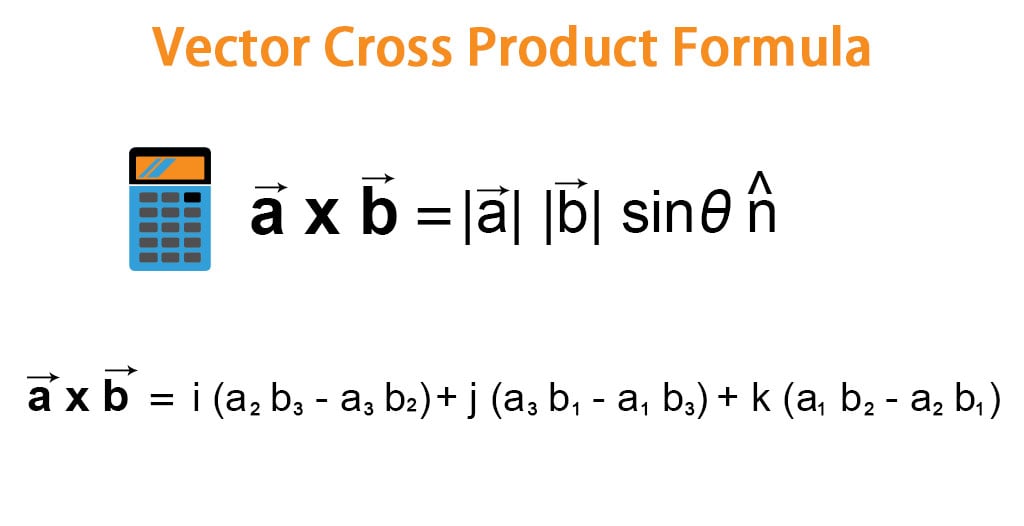


Vector Cross Product Formula Examples With Excel Template



Homework5solutions Pdf Name Gsi Disc Homework 5 Math 55 Fall 17 Prob 1 Find A Formula For Pm K 0 B 3 Kc Pm Solution First Note That Any Sum K 0 F K Course Hero
The quadratic equation is an equation of the form \a x^2 b x c = 0\ with \( a \neq 0\) It has solutions of the form \x = \frac{b \pm \sqrt{b^2 4ac}}{2a}\ In order to analyze the nature of the solution, the discriminant is defined as \D = b^2 4ac\The blue part ( b 2 4ac ) is called the "discriminant", because it can "discriminate" between the possible types of answerLogin Create Account Class8 » Math Algebraic Expressions and Identities what is formula of a 3 b 3 Share with your friends Share 1381


Www3 Mdc Edu Arcos Documents Chm1025 Chm1025 Exam3 Pdf
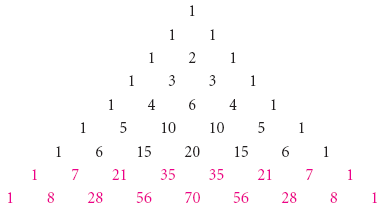


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
11 Factoring a 3b 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2 ab b 2) Proof (ab)•(a 2 abb 2) = a 3 a 2 b ab 2ba 2b 2 ab 3 = a 3 (a 2 bba 2)(ab 2b 2 a)b 3 = a 3 0 0b 3 = a 3b 3 Check a 3 is the cube of a 1 Check b 3 is the cube of b 1 Factorization is (a b) • (a 2 ab b 2)Q = (x 2;y 2) you can obtain the following information 1The distance betweenMathematics Formula Sheet Area of a square A = s2 rectangle A = lw parallelogram A = bh triangle !A = !



Excel Conditional Formatting With Formula Xelplus Leila Gharani


Math Berkeley Edu Peyam Math54sp15 Homeworks Homework 3 solutions Pdf
MATHEMATICAL FORMULAE Algebra MATHEMATICAL FORMULAE Algebra 1 (ab)2=a22abb2;a2b2=(ab)2−2ab 2 (a−b)2=a2−2abb;a2b2=(a−b)22ab 3 (abc)2=a2b2c22(abbcca) 4 (ab)3=a3b33ab(ab);a3b3=(ab)−3ab(ab) 5QuickMath allows students to get instant solutions to all kinds of math problems, from algebra and equation solving right through to calculus and matricesQ = (x 2;y 2) you can obtain the following information 1The distance between


A B 3 Formula And Example Lunlun Com


2
Knowledge of the quadratic formula is older than the Pythagorean Theorem Solving a cubic equation, on the other hand, was the first major success story of Renaissance mathematics in Italy The solution was first published by Girolamo Cardano () in his Algebra book Ars MagnaIf a b = 12 and a 3 b 3 = 468, then find the value of ab Solution To find the value of ab, we can use the formula or expansion for (a b) 3 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Substitute 12 for (a b) and 468 for (a 3 b 3)If you require all real and complex solutions, use the known solution to factor A^3 A 60 = ()(A^2 4A 15) The quadratic factor has no real roots, but its two complex solutions can be found via the quadratic formula



Rbse Solutions For Class 12 Maths Chapter 13 Vector Ex 13 5 In Class 12 Maths 12th Maths Studying Math



Solved Least Squares Solution Formula X Ata Atb Fo Chegg Com
Fermat's Last Theorem (from hereby referred to as FLT) states that In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b, and c can satisfy the equat(ab) * (ab) = a 2 ab ba b 2 = a 2 2ab b 2 But how did this equation a plus b whole square became generalized Let's prove this formula geometrically( Please refer to the pictures on the side) Consider a line segment Consider any arbitrary point on the line segment and name the first part as 'a' and the second part as 'b'3 To name Cr 2O 3 1 Determine the charge of cation from the anion (O2) 2 Cr ions 3 O2= 0 2 Cr ions 3 (2) = 0 2 Cr ions 6 = 0 2 Cr ions = 6 Cr ion = 3 = Cr3 2 Name the cation by the element name and add a Roman numeral in parenthesis to show its charge Cr3 = chromium(III) 3 Write the anion with an ide ending



Using Section Formula Show That The Points A 2 3 4 B 1 2 1 And C 0 1 3 2 Are Collinear Mathematics Shaalaa Com


The 3 Step Formula For Creating An A B Testing Hypothesis
If B2 C2 = 250 and Ab Ca = 3, Find a B C Mathematics Answer in Brief If a 2 b 2 c 2 = 250 and ab bc ca = 3, find a b c Advertisement Remove all ads Solution Show Solution Recall the formula `(abc)^2 = a^2 b^2 c^2 2(ab bc ca)` Given that `a^2 b^2 c^2 = 250 , ab bc ca = 3 ` CBSE PreviousGrade 3 » Operations & Algebraic Thinking » Understand properties of multiplication and the relationship between multiplication and division » 6 Print this page Understand division as an unknownfactor problem For example, find 32 ÷ 8 by finding the number that makes 32 when multiplied by 8This formula is the solution of a seconddegree polynomial equation The standard form of a quadratic equation is mentionedbelow ax 1 bx c = 0 Where;


Http Www Sd308 Org Cms Lib8 Il Centricity Domain 3273 Section 9 5 book even answers Pdf



Wk 1 Exercises With Solutions Studocu
Example Use the Quadratic Formula to solve Solution We have a=2, b= 3, and By the quadratic formula, the solutions are Please go to General Conclusion to find a summary of all the cases regarding the roots of a quadratic equation Complex Variables Trigonometry DifferentialAlgebra Formula Algebra includes both numbers and letters Numbers are fixed, ie their value is known Letters or alphabets are used to represent the unknown quantities in the algebra formula Now, a combination of numbers, letters, factorials, matrices etc is used to form an equation or formula This is essentially the methodology for algebraA quicker than trivial solution is as follows You calculate all values that a^3 b^3 can have, and store all possible values of a and b with it This is done by looping through a and b, storing the results (a^3 b^3) in a binary tree and having a list of values (a's and b's) associated to each result



The Quadratic Formula Solving Quadratic Equations Ppt Download



Predict The Number Of Ions Produced Per Formula Unit In An Aqueous
In algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers For example, a cannot be 0, or the equation would be linearThe section formula tells us the coordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio m n mn m n The midpoint of a line segment is the point that divides a line segment in two equal halves The section formula builds on it and is a more powerful tool;What is the formula for (a^3 b^3)?



Answered If We Solve The Equation B 3 4 5 T Bartleby



Solved Need To Help For The Formula 3 Month Rolling Sum Microsoft Power Bi Community
Step 2 Identify a, b, and c and plug them into the quadratic formula In this case a = 3, b = 4, and c = 8 Step 3 Use the order of operations to simplify the quadratic formula Step 4 Simplify the radical, if you can In this case you can simply the radical and remember that the square root of a negative number results in an imaginary≈314 Surface area and volume of aShows you the stepbystep solutions using the quadratic formula!



Solve Quadratic Equation With Step By Step Math Problem Solver


Uccs Edu Goman Sites Goman Files Inline Files 2150hw6solutions 3 Pdf
Compare the solutions of 2x 2 – 4x – 3 = 0 with the xintercepts of the graph Just as in the previous example, the xintercepts match the zeroes from the Quadratic Formula This is always true The "solutions" of an equation are also the xintercepts of the corresponding graphI guess another way of looking at it would be (ab)^3 = a^3 b^3 3(a^2)b 3a(b^2) Remember this formula It is simpler P now, to find the value of a^3 b^3, we move all the other terms to the left which gives us (ab)^3 (3(a^2)b 3a(bCompare the solutions of 2x 2 – 4x – 3 = 0 with the xintercepts of the graph Just as in the previous example, the xintercepts match the zeroes from the Quadratic Formula This is always true The "solutions" of an equation are also the xintercepts of the corresponding graph


Http Www Phxhs K12 Az Us Cms Lib6 Az Centricity Domain 6043 Unit 3 review part 1 Solving Pdf



A Cube Plus B Cube Algebra Identity Derivation Youtube
Notice that the formula is built up from the coe–cients a, b and c The same is true for cubic and quartics we build the solution starting from the coe–cients, and then using the operations of addition, subtraction, multiplication, division, and nth roots This process of flnding the solution is called a solution by radicals
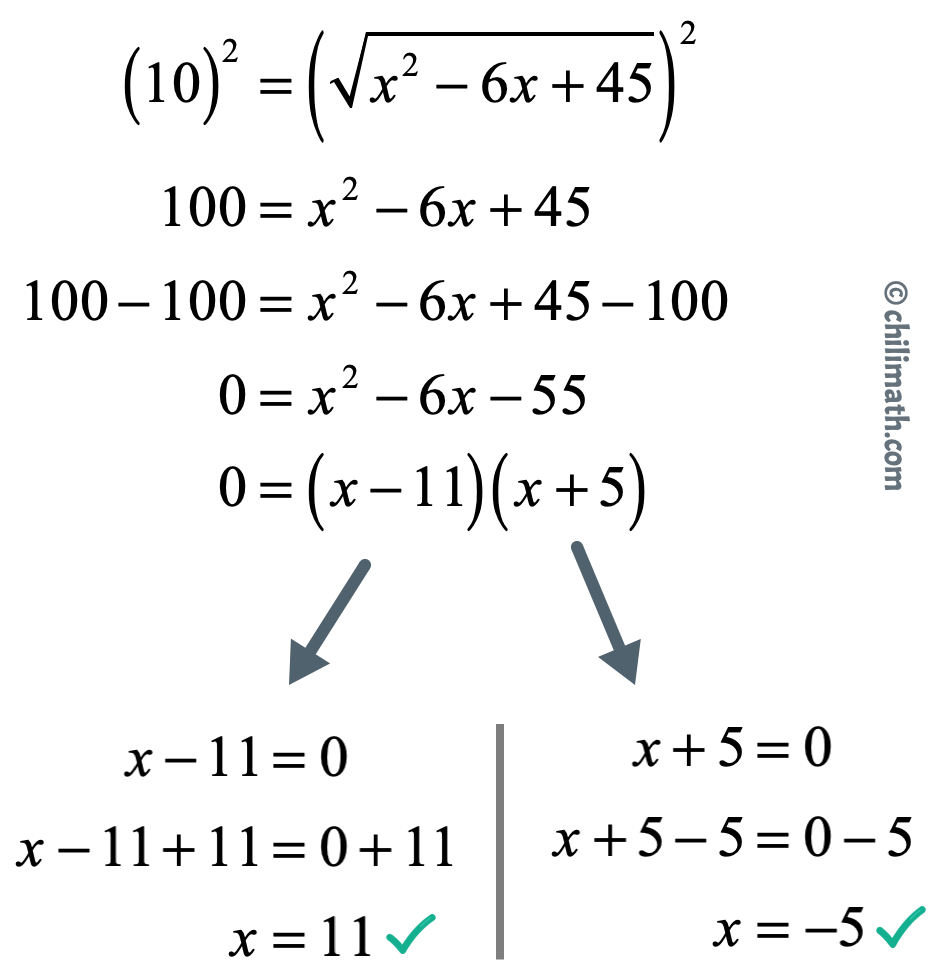


Distance Formula Chilimath
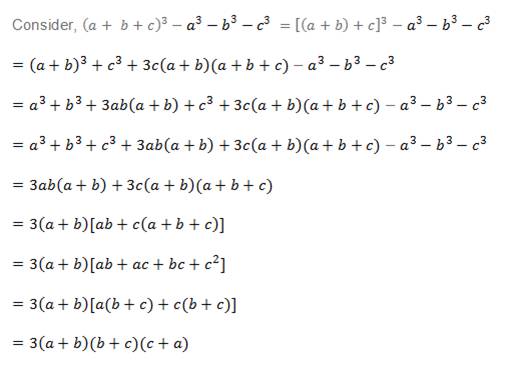


Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9



Solved 12 6 12 6 3 2 Let A 3 2 And B 3 2 6 6 3 6 Chegg Com


Niacinamide 5 Face Serum Advanced Formula With 5 Niacinamide Vitamin For Younger Plumper Firmer Skin Organic Natural Base Organic Content 62 Skin Beauty Solutions Professional Skin Care



Solved 2 6 3 2 Let A 32 And B 3 2 6 16 3 2 A 4 Chegg Com


Pages Uoregon Edu Belias Classes 253 Winter 19 Hw9 Solutions Pdf


Http Www Teaching Martahidegkuti Com Shared Lnotes 3 Algebra2 Line Equation Equation Pdf


Faculty Math Illinois Edu Hildebr 370 370generalproblemssol Pdf



If 0 A 3 0 B 3 And The Equation X2 4 3cos Ax B 2x Has At Least One S Askiitians


A 3 B 3 Formula And Example Lunlun Com


2



Solve By Quadratic Formula 9x 2 3 A B X Ab 0 Math Quadratic Equations Meritnation Com


Www Maths Gla Ac Uk Dvaleri 17 18 Final Training Solutions Pdf


2



Amazon Com Niacinamide 5 Face Serum Advanced Formula With 5 Niacinamide Vitamin For Younger Plumper Firm 4 Oz 1 Ml Beauty



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo


Multiplying Algebraic Expressions Solutions Examples Videos


Solution A Find The Equation Of The Line Through The Points A 0 4 And B 3 2 B Find L The Equation Of The Line Through B And Is Perpendicular To Ab C


2


2


Http Thewe Net Math Gelfand Gelfand3 Pdf



Factoring Special Binomials



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets


What Point On X Axis Is Equidistant From The Points A 7 6 And B 3 4 Coordinate Geometry Maths Class 10



What Is The Answer Of This Formula A B 3 Mathematics Topperlearning Com O2bgc4vv



What Is The Formula Of Math A B 3 Math Quora



The Quadratic Formula Algebra Video Khan Academy


Http Mit Edu 18 06 Www Spring10 Pset1 S10 Soln Pdf



Section And Mid Point Formula Solutions For Icse Board Class 10 Mathematics Concise Selina Publishers


The Quadratic Formula Explained Purplemath



Section 8 4 Quadratic Formula Ppt Video Online Download


What Is The Formula Of Math A B 3 Math Quora



Factoring Special Binomials



Solutions To Quiz 5 Questions Elementary Differential Equations Math 3 Docsity



Mathematics Class 9th Chapter 4 Solution


Is There A Systematic Way Of Solving Cubic Equations Mathematics Stack Exchange



Formula Of Ab 3 Is Please Answer This Brainly In
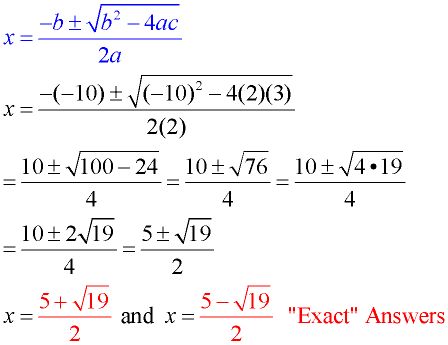


Quadratic Formula Mathbitsnotebook A1 Ccss Math



How To Solve Perfectly Cubed Equations Video Lesson Transcript Study Com


Herons Formula Explained With Pictures Examples And Practice Problems


What Is A B 3 Quora


Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau


Http Www Stevens Edu Ssm Feb5 Pdf


Search Q A B Whole Cube Tbm Isch



Minimum Formula For 3 X3x3 Rubik Cube Solution Last Layer Permutat


Search Q A3 Tbm Isch



Excel If And Or Functions Explained My Online Training Hub



Rbse Solutions For Class 12 Maths Chapter 13 Vector Ex 13 5 Class 12 Maths Studying Math 12th Maths


Http Thewe Net Math Gelfand Gelfand3 Pdf


Www Lcps Org Cms Lib Va Centricity Domain 562 Unit 3 day 9 quadratic regression flip Pdf



Quartic Function Wikipedia



Algebra Assessment Solutions Algebra And


Subsets Video Lessons Examples And Solutions



Solve Quadratic Equation With Step By Step Math Problem Solver
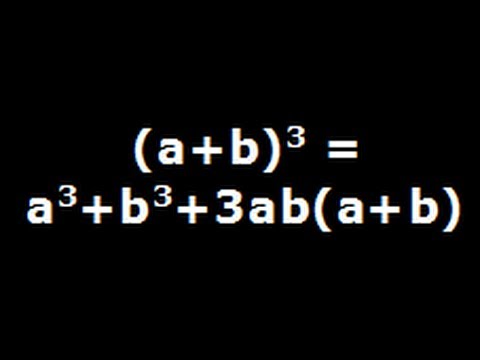


A Plus B Cube Algebra Identity Explained Step By Step Youtube


2


Courses Math Tufts Edu Math42 Exams S10final Sol Pdf



Algebra Homework Help And Exam Questions Page 986
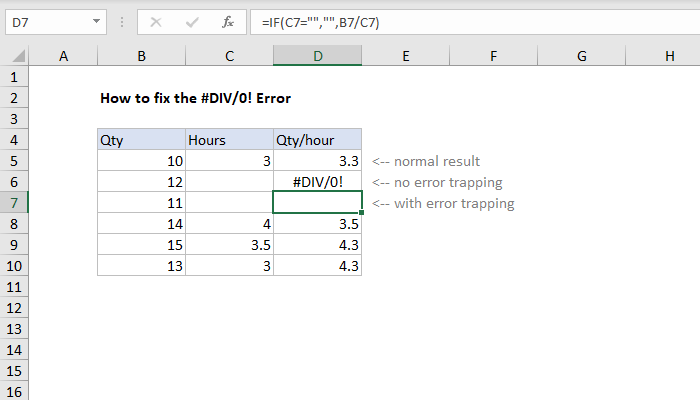


Excel Formula How To Fix The Div 0 Error Exceljet



Using The Quadratic Formula Number Of Solutions Video Khan Academy



Hw3 Solution
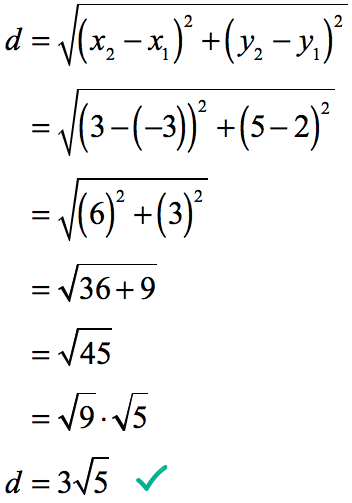


Distance Formula Chilimath



Selina Concise Mathematics Class 10 Icse Solutions Section And Mid Point Formula A Plus Topper


Http Lancasterschools Org Cms Lib Ny Centricity Domain 250 Algebra ccls Fe review R6 Linear graphing 14 Pdf
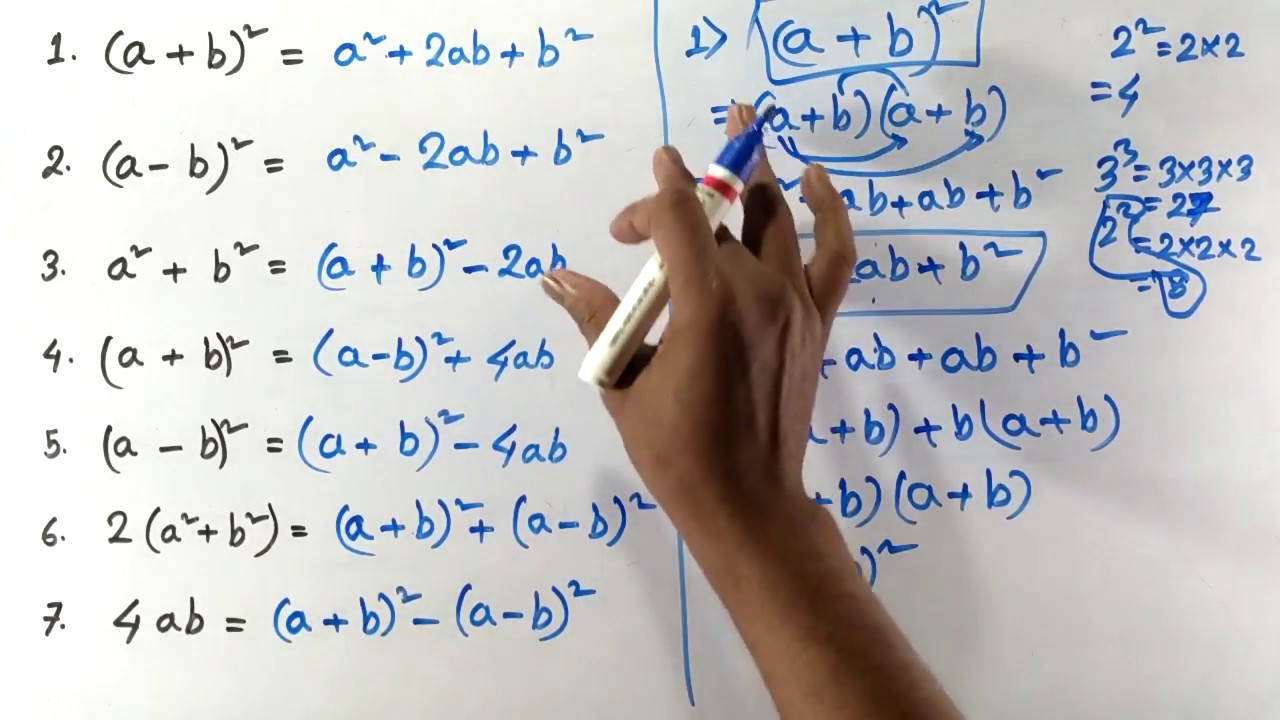


What Is Algebraic Formulas How To Remember Easily In Hindi Youtube


Math Scene Equations Iii Lesson 1 Quadratic Equations


Www Depts Ttu Edu Math Undergraduate Finalexams Math13 Math13 17spring Pdf



Prove That A3 C3 3abc A B C B2 C2 Ab Ac By Taking Lhs Brainly In


コメント
コメントを投稿